| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 6 Lines And Angles
Welcome to this comprehensive resource providing detailed solutions for the NCERT Exemplar problems specifically designed for Class 9 Mathematics, Chapter 6: Lines and Angles. These Exemplar questions represent a significant step up in complexity compared to standard textbook exercises. They are meticulously crafted to challenge students' understanding of fundamental geometric principles, demanding stronger deductive reasoning skills and the ability to apply angle theorems accurately and strategically within intricate geometric figures, often involving multiple intersecting and parallel lines. The primary goal is to move beyond mere calculation towards genuine geometric proof and rigorous problem-solving.
The solutions provided begin by reinforcing basic angle concepts, such as types of angles, adjacent angles, the critical Linear Pair Axiom (angles on a straight line sum to $180^\circ$), and the properties of vertically opposite angles (formed by intersecting lines, they are always equal). However, the core focus swiftly transitions to the more complex relationships arising from parallel lines intersected by a transversal. The solutions thoroughly explain and demonstrate the application of the following key angle pairs when lines are parallel:
- Corresponding Angles Axiom: Angles in corresponding positions are equal.
- Alternate Interior Angles Theorem: Angles on opposite sides of the transversal and between the parallel lines are equal.
- Alternate Exterior Angles Theorem: Angles on opposite sides of the transversal and outside the parallel lines are equal.
- Consecutive Interior Angles Theorem (Co-interior angles): Angles on the same side of the transversal and between the parallel lines are supplementary (sum to $180^\circ$).
Equally important, and rigorously applied in the solutions, are the converse theorems. These allow students to prove that two lines are parallel if a pair of corresponding angles, alternate interior angles, or alternate exterior angles are equal, or if a pair of consecutive interior angles are supplementary. Mastering both the direct application and the converse is essential for geometric reasoning.
Furthermore, the solutions integrate the fundamental properties of triangles, recognizing their frequent interplay with parallel line scenarios:
- The indispensable Angle Sum Property of a Triangle, stating that the sum of the interior angles of any triangle is always $180^\circ$.
- The Exterior Angle Theorem, asserting that the measure of an exterior angle of a triangle equals the sum of the measures of its two opposite interior angles.
The true challenge of the Exemplar problems often lies in their intricate design. Diagrams may feature multiple parallel lines intersected by several transversals, requiring students to carefully identify the relevant lines and angle pairs, apply theorems sequentially in a multi-step process, or sometimes even introduce auxiliary construction lines (e.g., drawing a line parallel to given lines through a crucial vertex) to facilitate the solution. A significant emphasis is also placed on writing formal, logical proofs for geometric statements involving angles and parallel lines.
Addressing diverse question formats (MCQs, Fill-in-the-Blanks, T/F, Short/Long Answer), these solutions offer clearly annotated diagrams, meticulous step-by-step derivations for finding unknown angles, and crucially, provide precise geometric justifications for each step by explicitly citing the relevant axiom or theorem (e.g., "using Alternate Interior Angles Theorem," "by Linear Pair Axiom," "applying Angle Sum Property"). For proof-based questions, structured, logical arguments are presented. Engaging with this resource is vital for students aiming to master geometric problem-solving involving lines and angles and to develop the rigorous proof techniques necessary for higher mathematics.
Sample Question 1 (Before Exercise 6.1)
Write the correct answer:
Sample Question 1: If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2 : 3, then the greater of the two angles is
(A) 54°
(B) 108°
(C) 120°
(D) 136°
Answer:
Given:
Two parallel lines intersected by a transversal.
Two interior angles on the same side of the transversal are in the ratio $2 : 3$.
To Find:
The greater of the two angles.
Solution:
Let the two interior angles on the same side of the transversal be $2x$ and $3x$, based on the given ratio $2 : 3$.
We know that when a transversal intersects two parallel lines, the sum of the interior angles on the same side of the transversal is $180^\circ$. These are called consecutive interior angles.
Sum of consecutive interior angles $= 180^\circ$
So, we can write the equation:
$2x + 3x = 180^\circ$
... (i)
Combine like terms:
$5x = 180^\circ$
Solve for $x$:
$x = \frac{180^\circ}{5}$
$x = 36^\circ$
Now, we find the values of the two angles:
First angle $= 2x = 2 \times 36^\circ = 72^\circ$
Second angle $= 3x = 3 \times 36^\circ = 108^\circ$
The two angles are $72^\circ$ and $108^\circ$.
We need to find the greater of the two angles.
Comparing $72^\circ$ and $108^\circ$, the greater angle is $108^\circ$.
The greater of the two angles is $108^\circ$.
This corresponds to option (B).
Exercise 6.1
Write the correct answer in each of the following:
Question 1. In Fig. 6.1, if AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°, then ∠QRS is equal to

(A) 85°
(B) 135°
(C) 145°
(D) 110°
Answer:
Given:
In the given figure, we have:
AB || CD || EF
PQ || RS
$\angle RQD = 25^\circ$
$\angle CQP = 60^\circ$
To Find:
The value of $\angle QRS$.
Construction Required:
Extend the line segment QP backwards to intersect the line AB at a point Y.
Solution:
We are given that AB || CD, and the line PY acts as a transversal intersecting them at Y and Q respectively.
The angles $\angle AYQ$ and $\angle CQP$ are corresponding angles. When two parallel lines are intersected by a transversal, the corresponding angles are equal.
$\angle AYQ = \angle CQP$
[Corresponding angles]
Since we are given $\angle CQP = 60^\circ$, it follows that:
$\angle AYQ = 60^\circ$
... (i)
Since AB is a straight line, the angles $\angle AYQ$ and $\angle BYQ$ form a linear pair.
$\angle AYQ + \angle BYQ = 180^\circ$
[Linear Pair]
$60^\circ + \angle BYQ = 180^\circ$
$\angle BYQ = 180^\circ - 60^\circ = 120^\circ$
... (ii)
Now, we are given that PQ || RS, which means the line PY is parallel to the line RS. The line AB acts as a transversal intersecting these parallel lines at Y and R.
The angles $\angle BYQ$ and $\angle ARS$ are alternate interior angles. Therefore, they are equal.
$\angle ARS = \angle BYQ$
[Alternate interior angles]
$\angle ARS = 120^\circ$
... (iii)
Also, we are given that AB || CD, and the line RQ is a transversal.
The angles $\angle ARQ$ and $\angle RQD$ are alternate interior angles. Therefore, they are equal.
$\angle ARQ = \angle RQD$
[Alternate interior angles]
$\angle ARQ = 25^\circ$
... (iv)
From the figure, the angle $\angle QRS$ is the sum of the adjacent angles $\angle ARS$ and $\angle ARQ$.
$\angle QRS = \angle ARS + \angle ARQ$
Substituting the values from equations (iii) and (iv):
$\angle QRS = 120^\circ + 25^\circ$
$\angle QRS = 145^\circ$
Hence, the value of $\angle QRS$ is 145°.
The correct option is (C) 145°.
Question 2. If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
(A) an isosceles triangle
(B) an obtuse triangle
(C) an equilateral triangle
(D) a right triangle
Answer:
Given:
In a triangle ABC, one angle is equal to the sum of the other two angles.
To Determine:
The type of triangle.
Solution:
Let the angles of the triangle be $\angle A$, $\angle B$, and $\angle C$.
According to the problem statement, assume one angle, say $\angle A$, is equal to the sum of the other two angles, $\angle B$ and $\angle C$.
$\angle A = \angle B + \angle C$
[Given] ... (i)
By the Angle Sum Property of a Triangle, the sum of all three angles in a triangle is $180^\circ$.
$\angle A + \angle B + \angle C = 180^\circ$
[Angle Sum Property]
Substitute the value of $(\angle B + \angle C)$ from equation (i) into the Angle Sum Property equation:
$\angle A + \angle A = 180^\circ$
$2\angle A = 180^\circ$
Solve for $\angle A$:
$\angle A = \frac{180^\circ}{2}$
$\angle A = 90^\circ$
Since one angle of the triangle is $90^\circ$, the triangle is a right triangle.
The correct option is (D) a right triangle.
Question 3. An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is
(A) $37\frac{1}{2}^\circ$
(B) $52\frac{1}{2}^\circ$
(C) $72\frac{1}{2}^\circ$
(D) $75^\circ$
Answer:
Given:
An exterior angle of a triangle is $105^\circ$.
The two interior opposite angles are equal.
To Find:
The measure of each of the equal interior opposite angles.
Solution:
Let the triangle be ABC. Let the exterior angle at vertex C be $105^\circ$. The interior opposite angles to this exterior angle are $\angle A$ and $\angle B$.
According to the Exterior Angle Property of a Triangle, the measure of an exterior angle of a triangle is equal to the sum of the measures of its two interior opposite angles.
Exterior angle at C = $\angle A + \angle B$
[Exterior Angle Property]
We are given that the exterior angle at C is $105^\circ$. So,
$\angle A + \angle B = 105^\circ$
... (i)
We are also given that the two interior opposite angles are equal. So, $\angle A = \angle B$.
$\angle A = \angle B$
[Given]
Substitute $\angle B = \angle A$ into equation (i):
$\angle A + \angle A = 105^\circ$
$2\angle A = 105^\circ$
Solve for $\angle A$:
$\angle A = \frac{105^\circ}{2}$
$\angle A = 52.5^\circ$
Since $\angle A = \angle B$, $\angle B = 52.5^\circ$.
The fraction form of $52.5^\circ$ is $52\frac{1}{2}^\circ$.
The measure of each of the equal angles is $52\frac{1}{2}^\circ$.
The correct option is (B) $52\frac{1}{2}^\circ$.
Question 4. The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is
(A) an acute angled triangle
(B) an obtuse angled triangle
(C) a right triangle
(D) an isosceles triangle
Answer:
Given:
The angles of a triangle are in the ratio 5 : 3 : 7.
To Determine:
The type of triangle.
Solution:
Let the angles of the triangle be $5x$, $3x$, and $7x$, where $x$ is a common multiple.
The sum of the angles in a triangle is $180^\circ$ (Angle Sum Property of a Triangle).
$5x + 3x + 7x = 180^\circ$
[Angle Sum Property]
Combine the terms on the left side:
$(5 + 3 + 7)x = 180^\circ$
$15x = 180^\circ$
Now, solve for $x$:
$x = \frac{180^\circ}{15}$
$\frac{\cancel{180}^{12}}{\cancel{15}_{1}}$
$x = 12^\circ$
Now, find the measure of each angle:
First angle $= 5x = 5(12^\circ) = 60^\circ$
Second angle $= 3x = 3(12^\circ) = 36^\circ$
Third angle $= 7x = 7(12^\circ) = 84^\circ$
Check the measure of each angle:
$60^\circ < 90^\circ$ (Acute)
$36^\circ < 90^\circ$ (Acute)
$84^\circ < 90^\circ$ (Acute)
Since all three angles are acute angles (less than $90^\circ$), the triangle is an acute angled triangle.
Also, since no two angles are equal, it is not an isosceles triangle. Since no angle is $90^\circ$, it is not a right triangle. Since not all angles are $60^\circ$, it is not an equilateral triangle.
The correct option is (A) an acute angled triangle.
Question 5. If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be
(A) 50°
(B) 65°
(C) 145°
(D) 155°
Answer:
Given:
In a triangle, one of the angles is $130^\circ$.
To Find:
The angle between the bisectors of the other two angles.
Solution:
Let's consider a triangle $\triangle ABC$, where $\angle A = 130^\circ$.
Let BO and CO be the angle bisectors of $\angle B$ and $\angle C$ respectively. These bisectors meet at point O inside the triangle.
Since BO is the bisector of $\angle B$, we have:
$\angle OBC = \frac{1}{2}\angle B$
Similarly, since CO is the bisector of $\angle C$, we have:
$\angle OCB = \frac{1}{2}\angle C$
Now, let's apply the angle sum property in $\triangle ABC$:
$\angle A + \angle B + \angle C = 180^\circ$
[Sum of angles in a triangle is $180^\circ$]
Substitute the value of $\angle A = 130^\circ$:
$130^\circ + \angle B + \angle C = 180^\circ$
$\angle B + \angle C = 180^\circ - 130^\circ$
$\angle B + \angle C = 50^\circ$
... (i)
Now, let's apply the angle sum property in $\triangle BOC$:
$\angle BOC + \angle OBC + \angle OCB = 180^\circ$
Substituting the values of the bisected angles:
$\angle BOC + \frac{1}{2}\angle B + \frac{1}{2}\angle C = 180^\circ$
$\angle BOC + \frac{1}{2}(\angle B + \angle C) = 180^\circ$
From equation (i), we know that $\angle B + \angle C = 50^\circ$. Substituting this value:
$\angle BOC + \frac{1}{2}(50^\circ) = 180^\circ$
$\angle BOC + 25^\circ = 180^\circ$
$\angle BOC = 180^\circ - 25^\circ$
$\angle BOC = 155^\circ$
Alternate Solution:
There is a direct theorem for the angle formed by the intersection of the internal bisectors of two angles of a triangle.
If $\angle B$ and $\angle C$ are bisected by BO and CO respectively, then the angle $\angle BOC$ is given by the formula:
$\angle BOC = 90^\circ + \frac{1}{2}\angle A$
Given $\angle A = 130^\circ$:
$\angle BOC = 90^\circ + \frac{1}{2}(130^\circ)$
$\angle BOC = 90^\circ + 65^\circ$
$\angle BOC = 155^\circ$
The angle between the bisectors of the other two angles is $155^\circ$.
Hence, the correct option is (D) 155°.
Question 6. In Fig. 6.2, POQ is a line. The value of x is

(A) 20°
(B) 25°
(C) 30°
(D) 35°
Answer:
Given:
From the given figure (Fig. 6.2), we have:
POQ is a straight line.
The angles formed at point O on the line are $40^\circ$, $4x$, and $3x$.
To Find:
The value of x.
Solution:
Since POQ is a straight line, the sum of all the angles on one side of the line at point O must be $180^\circ$. This is a property of angles on a straight line (or Linear Pair Axiom).
Therefore, we can write the equation:
$40^\circ + 4x + 3x = 180^\circ$
[Angles on a straight line]
Now, we will solve this equation for x.
Combine the terms with x:
$40^\circ + 7x = 180^\circ$
Subtract $40^\circ$ from both sides of the equation:
$7x = 180^\circ - 40^\circ$
$7x = 140^\circ$
Divide both sides by 7 to find the value of x:
$x = \frac{140^\circ}{7}$
$x = 20^\circ$
Thus, the value of x is $20^\circ$.
Comparing our result with the options, we find that it matches option (A).
Hence, the correct option is (A) 20°.
Question 7. In Fig. 6.3, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠ PQR is equal to

(A) 40°
(B) 50°
(C) 60°
(D) 70°
Answer:
Given:
In the given figure, we have:
OP || RS
$\angle OPQ = 110^\circ$
$\angle QRS = 130^\circ$
To Find:
The measure of $\angle PQR$.
Construction Required:
Draw a line XY through the point Q, such that XY is parallel to OP and RS.
Solution:
According to the construction, we have OP || XY.
Consider the parallel lines OP and XY, with PQ as the transversal line.
The angles on the same side of the transversal (consecutive interior angles) are supplementary (add up to $180^\circ$).
$\angle OPQ + \angle PQX = 180^\circ$
[Consecutive Interior Angles]
Substitute the given value $\angle OPQ = 110^\circ$:
$110^\circ + \angle PQX = 180^\circ$
$\angle PQX = 180^\circ - 110^\circ$
$\angle PQX = 70^\circ$
... (i)
Now, consider the parallel lines RS and XY, with QR as the transversal line.
Again, the consecutive interior angles are supplementary.
$\angle QRS + \angle RQY = 180^\circ$
[Consecutive Interior Angles]
Substitute the given value $\angle QRS = 130^\circ$:
$130^\circ + \angle RQY = 180^\circ$
$\angle RQY = 180^\circ - 130^\circ$
$\angle RQY = 50^\circ$
... (ii)
Since XY is a straight line, the sum of angles at point Q on the line is $180^\circ$.
$\angle PQX + \angle PQR + \angle RQY = 180^\circ$
[Angles on a straight line]
Substitute the values from (i) and (ii):
$70^\circ + \angle PQR + 50^\circ = 180^\circ$
$120^\circ + \angle PQR = 180^\circ$
$\angle PQR = 180^\circ - 120^\circ$
$\angle PQR = 60^\circ$
The measure of $\angle PQR$ is $60^\circ$.
The correct option is (C) 60°.
Question 8. Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is
(A) 60°
(B) 40°
(C) 80°
(D) 20°
Answer:
Given:
The angles of a triangle are in the ratio 2 : 4 : 3.
To Find:
The measure of the smallest angle of the triangle.
Solution:
Let the angles of the triangle be $2x$, $4x$, and $3x$, where $x$ is a common multiple.
The sum of the angles in a triangle is $180^\circ$ (Angle Sum Property of a Triangle).
$2x + 4x + 3x = 180^\circ$
[Angle Sum Property]
Combine the terms on the left side:
$(2 + 4 + 3)x = 180^\circ$
$9x = 180^\circ$
Now, solve for $x$:
$x = \frac{180^\circ}{9}$
$\frac{\cancel{180}^{20}}{\cancel{9}_{1}}$
$\mathbf{x = 20^\circ}$
Now, find the measure of each angle:
First angle $= 2x = 2(20^\circ) = 40^\circ$
Second angle $= 4x = 4(20^\circ) = 80^\circ$
Third angle $= 3x = 3(20^\circ) = 60^\circ$
The angles of the triangle are $40^\circ$, $80^\circ$, and $60^\circ$.
The smallest angle among these is $40^\circ$.
The smallest angle of the triangle is $40^\circ$.
The correct option is (B) 40°.
Sample Question 1 & 2 (Before Exercise 6.2)
Sample Question 1: Let OA, OB, OC and OD are rays in the anticlockwise direction such that ∠ AOB = ∠COD = 100°, ∠BOC = 82° and ∠AOD = 78°. Is it true to say that AOC and BOD are lines?
Answer:
Given:
OA, OB, OC and OD are rays in the anticlockwise direction from a point O.
$\angle AOB = 100^\circ$
$\angle COD = 100^\circ$
$\angle BOC = 82^\circ$
$\angle AOD = 78^\circ$
To Find:
Whether AOC and BOD are lines.
Solution:
For AOC to be a straight line passing through O, the angle $\angle AOC$ must be $180^\circ$. Since the rays are given in anticlockwise direction, we can find $\angle AOC$ by adding the consecutive angles between OA and OC.
$\angle AOC = \angle AOB + \angle BOC$
Substitute the given values:
$\angle AOC = 100^\circ + 82^\circ$
$\angle AOC = 182^\circ$
Since $182^\circ \neq 180^\circ$, AOC is not a straight line.
Similarly, for BOD to be a straight line passing through O, the angle $\angle BOD$ must be $180^\circ$. Since the rays are given in anticlockwise direction, we can find $\angle BOD$ by adding the consecutive angles between OB and OD.
$\angle BOD = \angle BOC + \angle COD$
Substitute the given values:
$\angle BOD = 82^\circ + 100^\circ$
$\angle BOD = 182^\circ$
Since $182^\circ \neq 180^\circ$, BOD is not a straight line.
Therefore, it is not true to say that AOC and BOD are lines.
Sample Question 2: A transversal intersects two lines in such a way that the two interior angles on the same side of the transversal are equal. Will the two lines always be parallel? Give reason for your answer.
Answer:
Answer: No, it is not always true.
Reason:
When a transversal intersects two lines, the lines are parallel if and only if the sum of the interior angles on the same side of the transversal is $180^\circ$ (supplementary).
Let the two interior angles on the same side of the transversal be $\angle 1$ and $\angle 2$.
The condition for the lines to be parallel is $\angle 1 + \angle 2 = 180^\circ$.
The problem states that these two interior angles are equal, i.e., $\angle 1 = \angle 2$.
If we let $\angle 1 = \angle 2 = x$, then the condition for parallel lines becomes:
$x + x = 180^\circ$
$2x = 180^\circ$
$x = \frac{180^\circ}{2}$
$x = 90^\circ$
Thus, the two lines will be parallel only if both of the equal interior angles on the same side of the transversal are $90^\circ$. If they are equal but not $90^\circ$ (e.g., both are $60^\circ$), their sum is $120^\circ$, which is not $180^\circ$, and the lines will intersect on that side of the transversal.
Therefore, the lines are not always parallel just because the interior angles on the same side are equal. They are parallel only in the specific case where these equal angles are right angles ($90^\circ$).
Exercise 6.2
Question 1. For what value of x + y in Fig. 6.4 will ABC be a line? Justify your answer.
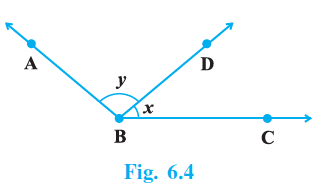
Answer:
Given:
A figure where points A, B, and C are arranged such that ABC might form a line, with angles involving measures x and y.
To Find:
The value of $x+y$ for which ABC is a line.
Solution:
For points A, B, and C to form a straight line with B lying between A and C, the angle formed by the rays BA and BC, which is $\angle ABC$, must be a straight angle.
A straight angle measures $180^\circ$.
From the figure (as implied by the structure of the question asking for the value of $x+y$), the angle $\angle ABC$ is composed of two adjacent angles with measures $x$ and $y$.
Thus, $\angle ABC = x + y$.
For ABC to be a line, we must have:
$\angle ABC = 180^\circ$
Substituting the expression for $\angle ABC$:
$x + y = 180^\circ$
Justification:
If the sum of two adjacent angles is $180^\circ$, then their non-common arms form a straight line. In this case, the angles with measures $x$ and $y$ are adjacent, and their non-common arms are the rays BA and BC. If their sum $x+y$ is $180^\circ$, then BA and BC are opposite rays, making ABC a straight line.
Therefore, for ABC to be a line, the value of $x+y$ must be $180^\circ$.
Question 2. Can a triangle have all angles less than 60°? Give reason for your answer.
Answer:
Answer: No.
Reason:
The sum of the interior angles of a triangle is always $180^\circ$. This is known as the Angle Sum Property of a triangle.
Let the three angles of a triangle be $\angle A$, $\angle B$, and $\angle C$.
According to the Angle Sum Property:
$\angle A + \angle B + \angle C = 180^\circ$
If all angles of the triangle were less than $60^\circ$, say:
$\angle A < 60^\circ$
$\angle B < 60^\circ$
$\angle C < 60^\circ$
Summing these inequalities, we get:
$\angle A + \angle B + \angle C < 60^\circ + 60^\circ + 60^\circ$
$\angle A + \angle B + \angle C < 180^\circ$
This contradicts the Angle Sum Property, which states that $\angle A + \angle B + \angle C$ must be exactly $180^\circ$.
Therefore, a triangle cannot have all angles less than $60^\circ$. At least one angle must be $60^\circ$ or greater.
Question 3. Can a triangle have two obtuse angles? Give reason for your answer.
Answer:
Answer: No.
Reason:
An obtuse angle is an angle that measures more than $90^\circ$.
Let the three angles of a triangle be $\angle A$, $\angle B$, and $\angle C$.
According to the Angle Sum Property of a triangle, the sum of the interior angles of any triangle is always $180^\circ$.
$\angle A + \angle B + \angle C = 180^\circ$
Suppose, for the sake of contradiction, that a triangle has two obtuse angles. Let these angles be $\angle A$ and $\angle B$.
Then, by definition of an obtuse angle:
$\angle A > 90^\circ$
$\angle B > 90^\circ$
Summing these two inequalities, we get:
$\angle A + \angle B > 90^\circ + 90^\circ$
$\angle A + \angle B > 180^\circ$
Now, consider the sum of all three angles of the triangle: $\angle A + \angle B + \angle C$.
Since $\angle C$ in a triangle must be a positive angle (an angle in a triangle cannot be zero or negative), $\angle C > 0^\circ$.
Adding $\angle C$ to the inequality $\angle A + \angle B > 180^\circ$, we get:
$\angle A + \angle B + \angle C > 180^\circ + \angle C$
Since $\angle C > 0^\circ$, it follows that:
$\angle A + \angle B + \angle C > 180^\circ$
This contradicts the Angle Sum Property of a triangle, which states that $\angle A + \angle B + \angle C$ must be exactly $180^\circ$.
Therefore, the assumption that a triangle can have two obtuse angles must be false.
A triangle can have at most one obtuse angle.
Question 4. How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
Answer:
Answer: Zero (0).
Reason:
The sum of the interior angles of any triangle is always $180^\circ$. This is a fundamental property of triangles, known as the Angle Sum Property.
Let's find the sum of the given angles:
Sum of angles $= 45^\circ + 64^\circ + 72^\circ$
Calculating the sum:
$\begin{array}{cc} & 4 & 5 \\ & 6 & 4 \\ + & 7 & 2 \\ \hline & 18 & 1 \\ \hline \end{array}$
The sum of the given angles is $181^\circ$.
Since the sum of the given angles ($181^\circ$) is not equal to $180^\circ$, these angles cannot be the interior angles of a triangle.
Therefore, it is not possible to draw any triangle having angles measuring $45^\circ$, $64^\circ$, and $72^\circ$.
Question 5. How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
Answer:
Answer: Infinitely many.
Reason:
The sum of the interior angles of any triangle is always $180^\circ$. This is the Angle Sum Property of a triangle.
Let's find the sum of the given angles:
Sum of angles $= 53^\circ + 64^\circ + 63^\circ$
Calculating the sum:
$\begin{array}{cc} & 5 & 3 \\ & 6 & 4 \\ + & 6 & 3 \\ \hline & 18 & 0 \\ \hline \end{array}$
The sum of the given angles is $180^\circ$.
Since the sum of the given angles is exactly $180^\circ$, these angles can form a triangle.
If three angles can form a triangle, then any triangle with these angles will be similar to any other triangle with the same angles (by AAA similarity criterion).
Triangles having the same set of angles but different side lengths are similar. We can scale a triangle with these angles up or down to create triangles of different sizes while keeping the angles the same.
For example, we can draw a triangle with sides $a, b, c$ having these angles. We can then draw another triangle with sides $2a, 2b, 2c$ (if such a triangle exists with these angles, which it does if the original one exists), which will have the same angles but be larger. Similarly, we can draw triangles with sides $ka, kb, kc$ for any positive value of $k$.
Therefore, there are infinitely many triangles that can be drawn having angles $53^\circ$, $64^\circ$, and $63^\circ$. They will all be similar to each other but can have different sizes.
Question 6. In Fig. 6.5, find the value of x for which the lines l and m are parallel.
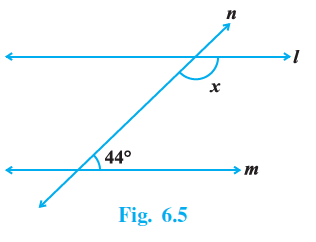
Answer:
To Find:
The value of x for which the lines l and m are parallel.
Solution:
For two lines to be parallel, when they are intersected by a transversal, the sum of the interior angles on the same side of the transversal (consecutive interior angles) must be supplementary, i.e., their sum must be $180^\circ$.
In the given figure, the lines are l and m, and n is the transversal. The angles marked as $x$ and $44^\circ$ are consecutive interior angles.
For the lines l and m to be parallel, the following condition must be met:
$x + 44^\circ = 180^\circ$
[Sum of consecutive interior angles is $180^\circ$]
Now, we can solve for x by subtracting $44^\circ$ from both sides:
$x = 180^\circ - 44^\circ$
$x = 136^\circ$
Thus, for the lines l and m to be parallel, the value of x must be 136°.
Question 7. Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
Answer:
Answer: No.
Justification:
Adjacent angles share a common vertex and a common arm. Let the two equal adjacent angles be $\angle A$ and $\angle B$, such that $\angle A = \angle B$.
It is not necessary that each of these angles will be a right angle ($90^\circ$).
Consider two adjacent angles, both measuring $45^\circ$. They are equal and adjacent, but they are not right angles.
$\angle A = 45^\circ$
$\angle B = 45^\circ$
Here, $\angle A = \angle B$, and they are adjacent. However, neither $\angle A$ nor $\angle B$ is a right angle.
The only situation where two equal adjacent angles are necessarily right angles is when their non-common arms form a straight line. In this case, the two adjacent angles form a linear pair, and their sum is $180^\circ$.
If $\angle A$ and $\angle B$ form a linear pair and $\angle A = \angle B$, then:
$\angle A + \angle B = 180^\circ$
Since $\angle A = \angle B$, we have:
$\angle A + \angle A = 180^\circ$
$2\angle A = 180^\circ$
$\angle A = \frac{180^\circ}{2}$
$\angle A = 90^\circ$
And since $\angle B = \angle A$, $\angle B = 90^\circ$.
So, if equal adjacent angles form a linear pair, they are right angles. But adjacent angles do not always form a linear pair. Therefore, it is not necessary for equal adjacent angles to be right angles.
Question 8. If one of the angles formed by two intersecting lines is a right angle, what can you say about the other three angles? Give reason for your answer.
Answer:
Given:
Two lines intersect.
One of the angles formed by the intersection is a right angle ($90^\circ$).
To Find:
What can be said about the other three angles.
Solution:
Let the two lines be $L_1$ and $L_2$, intersecting at point O. Let the four angles formed around O be $\angle 1, \angle 2, \angle 3,$ and $\angle 4$, taken in order.
Suppose $\angle 1$ is the right angle. So, $\angle 1 = 90^\circ$.
Angles $\angle 1$ and $\angle 2$ form a linear pair (adjacent angles on a straight line). Therefore, their sum is $180^\circ$.
$\angle 1 + \angle 2 = 180^\circ$
Substituting $\angle 1 = 90^\circ$:
$90^\circ + \angle 2 = 180^\circ$
$\angle 2 = 180^\circ - 90^\circ$
$\angle 2 = 90^\circ$
Similarly, angles $\angle 1$ and $\angle 4$ form a linear pair. Therefore, their sum is $180^\circ$.
$\angle 1 + \angle 4 = 180^\circ$
Substituting $\angle 1 = 90^\circ$:
$90^\circ + \angle 4 = 180^\circ$
$\angle 4 = 180^\circ - 90^\circ$
$\angle 4 = 90^\circ$
Angles $\angle 1$ and $\angle 3$ are vertically opposite angles. Vertically opposite angles are equal.
$\angle 3 = \angle 1$
Since $\angle 1 = 90^\circ$:
$\angle 3 = 90^\circ$
Alternatively, $\angle 2$ and $\angle 4$ are vertically opposite angles, and we found both are $90^\circ$, confirming this property.
Conclusion:
If one of the angles formed by two intersecting lines is a right angle, then all four angles are right angles ($90^\circ$). This means the two lines are perpendicular to each other.
Question 9. In Fig.6.6, which of the two lines are parallel and why?

Answer:
To determine which lines are parallel, we need to examine the relationship between the angles formed by the transversal line in each case. The key principle is the Converse of the Consecutive Interior Angles Theorem, which states that if two lines are cut by a transversal such that the sum of the consecutive interior angles is $180^\circ$, then the lines are parallel.
Case 1: Lines l and m intersected by transversal n
In the first figure, we are given two lines, l and m, and a transversal line, n.
The two interior angles on the same side of the transversal n are given as $132^\circ$ and $48^\circ$.
Let's find the sum of these consecutive interior angles:
Sum = $132^\circ + 48^\circ$
Sum = $180^\circ$
Since the sum of the consecutive interior angles is exactly $180^\circ$, the condition for the lines to be parallel is satisfied.
Therefore, line l is parallel to line m (l || m).
Case 2: Lines p and q intersected by transversal r
In the second figure, we are given two lines, p and q, and a transversal line, r.
The two interior angles on the same side of the transversal r are given as $73^\circ$ and $106^\circ$.
Let's find the sum of these consecutive interior angles:
Sum = $73^\circ + 106^\circ$
Sum = $179^\circ$
Since the sum of the consecutive interior angles is $179^\circ$, which is not equal to $180^\circ$, the condition for the lines to be parallel is not satisfied.
Therefore, line p is not parallel to line q.
Conclusion:
In Fig. 6.6, only the lines l and m are parallel because the sum of their consecutive interior angles is $180^\circ$.
Question 10. Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
Answer:
Answer: No.
Reason:
Let line $l$ be perpendicular to line $n$, and line $m$ be perpendicular to line $n$.
When a transversal intersects two lines such that the interior angles on the same side are supplementary, or corresponding angles are equal, or alternate interior angles are equal, then the two lines are parallel.
In this case, line $n$ acts as a transversal intersecting lines $l$ and $m$.
Since $l \perp n$, the angle between $l$ and $n$ is $90^\circ$.
Since $m \perp n$, the angle between $m$ and $n$ is $90^\circ$.
Consider the interior angles formed by lines $l$, $m$, and the transversal $n$ on the same side of $n$. Both these angles are $90^\circ$.
Their sum is $90^\circ + 90^\circ = 180^\circ$.
Since the sum of the interior angles on the same side of the transversal $n$ is $180^\circ$, lines $l$ and $m$ must be parallel to each other.
Parallel lines are lines that lie in the same plane and do not intersect.
Perpendicular lines are lines that intersect at a right angle ($90^\circ$).
Since lines $l$ and $m$ are parallel, they do not intersect (assuming they are distinct lines). Therefore, they cannot be perpendicular to each other.
Hence, if two lines are perpendicular to the same line, they are parallel to each other, not perpendicular to each other.
Sample Question 1 & 2 (Before Exercise 6.3)
Sample Question 1: In Fig. 6.7, AB, CD and EF are three lines concurrent at O. Find the value of y.
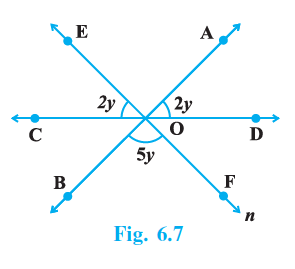
Answer:
Given:
In Fig. 6.7, three lines AB, CD, and EF intersect at a single point O (i.e., they are concurrent).
From the figure, we have the following angles:
$\angle COE = 2y$
$\angle AOD = 2y$
$\angle BOF = 5y$
To Find:
The value of y.
Solution:
When two lines intersect, the vertically opposite angles are equal. We will use this property to find all the angles around the point O in terms of y.
Since lines AB and EF intersect at O:
$\angle AOE = \angle BOF$
[Vertically opposite angles]
$\angle AOE = 5y$
... (i)
Since lines AB and CD intersect at O:
$\angle BOC = \angle AOD$
[Vertically opposite angles]
$\angle BOC = 2y$
... (ii)
Since lines CD and EF intersect at O:
$\angle DOF = \angle COE$
[Vertically opposite angles]
$\angle DOF = 2y$
... (iii)
Now, we know that the angles on a straight line add up to $180^\circ$. Let's consider the straight line CD.
The angles on the upper side of line CD are $\angle COE$, $\angle EOA$, and $\angle AOD$.
$\angle COE + \angle EOA + \angle AOD = 180^\circ$
[Angles on a straight line]
Substituting the values in terms of y from the given information and equation (i):
$2y + 5y + 2y = 180^\circ$
Combine the terms with y:
$9y = 180^\circ$
Solve for y:
$y = \frac{180^\circ}{9}$
$y = 20^\circ$
Thus, the value of y is 20°.
Alternate Solution:
The sum of all angles around a point is $360^\circ$.
Sum of angles = $\angle COE + \angle EOA + \angle AOD + \angle DOF + \angle FOB \ $$ + \angle BOC = 360^\circ$
From the previous solution, we know all the angles in terms of y:
$\angle COE = 2y$ (Given)
$\angle EOA = 5y$ (Vertically opposite to $\angle BOF$)
$\angle AOD = 2y$ (Given)
$\angle DOF = 2y$ (Vertically opposite to $\angle COE$)
$\angle FOB = 5y$ (Given)
$\angle BOC = 2y$ (Vertically opposite to $\angle AOD$)
Adding all these angles:
$2y + 5y + 2y + 2y + 5y + 2y = 360^\circ$
Combine the terms:
$18y = 360^\circ$
Solve for y:
$y = \frac{360^\circ}{18}$
$y = 20^\circ$
Both methods yield the same result, confirming that the value of y is 20°.
Sample Question 2: In Fig.6.8, x = y and a = b. Prove that l || n.

Answer:
Given:
Two lines l and m intersected by transversal p, forming angles $\angle x$ and $\angle y$ as shown in the figure.
Two lines m and n intersected by transversal q, forming angles $\angle a$ and $\angle b$ as shown in the figure.
$\angle x = \angle y$
$\angle a = \angle b$
To Prove:
Line l is parallel to line n (l || n).
Proof:
Consider lines l and m intersected by the transversal p.
The angles $\angle x$ and $\angle y$ are corresponding angles.
We are given that $\angle x = \angle y$.
$\angle x = \angle y$
[Given]
Since a pair of corresponding angles formed by transversal p with lines l and m is equal, the lines l and m must be parallel.
Therefore, l || m.
[Converse of Corresponding Angles Axiom] ... (i)
Now, consider lines m and n intersected by the transversal q.
The angles $\angle a$ and $\angle b$ are corresponding angles.
We are given that $\angle a = \angle b$.
$\angle a = \angle b$
[Given]
Since a pair of corresponding angles formed by transversal q with lines m and n is equal, the lines m and n must be parallel.
Therefore, m || n.
[Converse of Corresponding Angles Axiom] ... (ii)
From equation (i), we have l || m.
From equation (ii), we have m || n.
If two lines are parallel to the same line, then they are parallel to each other.
Since line l is parallel to line m, and line m is parallel to line n, it follows that line l is parallel to line n.
Therefore, l || n.
Hence, proved.
Exercise 6.3
Question 1. In Fig. 6.9, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear.
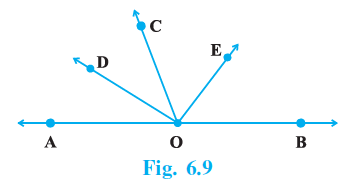
Answer:
Given:
OD is the bisector of $\angle AOC$.
OE is the bisector of $\angle BOC$.
$OD \perp OE$.
To Prove:
Points A, O and B are collinear (i.e., $\angle AOB = 180^\circ$).
Proof:
Since OD is the bisector of $\angle AOC$, we have:
$\angle DOC = \frac{1}{2}\angle AOC$
... (i)
This can also be written as $\angle AOC = 2\angle DOC$.
Since OE is the bisector of $\angle BOC$, we have:
$\angle COE = \frac{1}{2}\angle BOC$
... (ii)
This can also be written as $\angle BOC = 2\angle COE$.
We are given that $OD \perp OE$. Therefore,
$\angle DOE = 90^\circ$
... (iii)
From the figure, it is clear that $\angle DOE$ is the sum of $\angle DOC$ and $\angle COE$.
$\angle DOC + \angle COE = \angle DOE$
[Angle Addition Postulate]
Substituting the value from (iii) into the above equation:
$\angle DOC + \angle COE = 90^\circ$
Now consider the sum of $\angle AOC$ and $\angle BOC$.
$\angle AOC + \angle BOC = 2\angle DOC + 2\angle COE$
[From (i) and (ii)]
$\angle AOC + \angle BOC = 2(\angle DOC + \angle COE)$
Substitute the value of ($\angle DOC + \angle COE$) from the previous step:
$\angle AOC + \angle BOC = 2(90^\circ)$
$\angle AOC + \angle BOC = 180^\circ$
The angles $\angle AOC$ and $\angle BOC$ are adjacent angles, and their sum is $180^\circ$. This means they form a linear pair.
When two adjacent angles form a linear pair, their non-common arms form a straight line.
The non-common arms of $\angle AOC$ and $\angle BOC$ are OA and OB.
Therefore, OA and OB lie on the same straight line.
Hence, the points A, O and B are collinear.
Question 2. In Fig. 6.10, ∠1 = 60° and ∠6 = 120°. Show that the lines m and n are parallel.
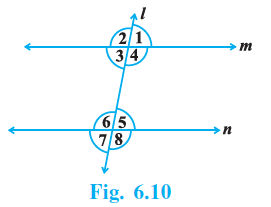
Answer:
Given:
$\angle 1 = 60^\circ$
$\angle 6 = 120^\circ$
To Show:
Lines m and n are parallel.
Proof:
From the figure, $\angle 1$ and $\angle 3$ are vertically opposite angles.
$\angle 3 = \angle 1$
[Vertically Opposite Angles]
Substituting the given value of $\angle 1$:
$\angle 3 = 60^\circ$
Now, consider the sum of $\angle 3$ and $\angle 6$. These are consecutive interior angles.
$\angle 3 + \angle 6 = 60^\circ + 120^\circ$
[Substituting values]
$\angle 3 + \angle 6 = 180^\circ$
Since the sum of the consecutive interior angles $\angle 3$ and $\angle 6$ is $180^\circ$, the lines m and n are parallel.
Thus, the lines m and n are parallel.
Question 3. AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (Fig. 6.11). Show that AP || BQ.
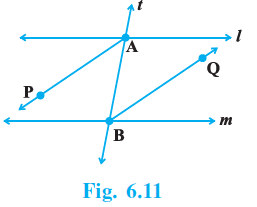
Answer:
Given:
Two parallel lines, l and m, are intersected by a transversal line, t, at points A and B, respectively.
The ray AP is the bisector of one alternate interior angle.
The ray BQ is the bisector of the other alternate interior angle.
l || m
To Prove:
The angle bisectors AP and BQ are parallel to each other.
AP || BQ
Proof:
Let's name the alternate interior angles as $\angle XAB$ and $\angle ABY$, where X is a point on line l and Y is a point on line m, as shown in the labeled figure.
We are given that line l is parallel to line m and they are intersected by the transversal t.
When two parallel lines are intersected by a transversal, the alternate interior angles are equal.
$\angle XAB = \angle ABY$
[Alternate interior angles] ... (i)
We are also given that AP is the bisector of $\angle XAB$.
This means that AP divides $\angle XAB$ into two equal halves.
$\angle PAB = \frac{1}{2} \angle XAB$
[AP bisects $\angle XAB$] ... (ii)
Similarly, we are given that BQ is the bisector of $\angle ABY$.
This means that BQ divides $\angle ABY$ into two equal halves.
$\angle ABQ = \frac{1}{2} \angle ABY$
[BQ bisects $\angle ABY$] ... (iii)
From equation (i), we have $\angle XAB = \angle ABY$.
If we take half of both angles, they will also be equal.
$\frac{1}{2} \angle XAB = \frac{1}{2} \angle ABY$
Now, substituting the values from equations (ii) and (iii) into the above equation, we get:
$\angle PAB = \angle ABQ$
Let's consider the lines AP and BQ with the line segment AB (which is a part of the transversal t) as a new transversal.
We have just proved that the angles $\angle PAB$ and $\angle ABQ$ are equal. These two angles form a pair of alternate interior angles for the lines AP and BQ.
According to the Converse of the Alternate Interior Angles Theorem, if two lines are cut by a transversal such that a pair of alternate interior angles is equal, then the two lines must be parallel.
Since $\angle PAB = \angle ABQ$, we can conclude that the lines AP and BQ are parallel.
AP || BQ
Hence, proved.
Question 4. If in Fig. 6.11, bisectors AP and BQ of the alternate interior angles are parallel, then show that l || m.
Answer:
Given:
Lines l and m are intersected by a transversal t at points A and B.
AP is the bisector of one alternate interior angle.
BQ is the bisector of the other alternate interior angle.
The bisectors are parallel to each other.
AP || BQ
To Prove:
The lines l and m are parallel.
l || m
Proof:
We are given that the line AP is parallel to the line BQ, and the transversal t (containing segment AB) intersects them.
When two parallel lines are intersected by a transversal, the alternate interior angles formed are equal.
In this case, for the parallel lines AP and BQ, the angles $\angle PAB$ and $\angle ABQ$ form a pair of alternate interior angles.
$\angle PAB = \angle ABQ$
[Alternate interior angles] ... (i)
Now, it is also given that AP is the bisector of the angle we can call $\angle XAB$.
This means that the whole angle $\angle XAB$ is twice the bisected angle $\angle PAB$.
$\angle XAB = 2 \times \angle PAB$
[AP is the angle bisector] ... (ii)
Similarly, BQ is the bisector of the angle we can call $\angle ABY$.
This means that the whole angle $\angle ABY$ is twice the bisected angle $\angle ABQ$.
$\angle ABY = 2 \times \angle ABQ$
[BQ is the angle bisector] ... (iii)
From equation (i), we know that $\angle PAB = \angle ABQ$.
Multiplying both sides of equation (i) by 2, we get:
$2 \times \angle PAB = 2 \times \angle ABQ$
Now, substituting the values from equations (ii) and (iii) into this equation, we obtain:
$\angle XAB = \angle ABY$
Let's now consider the original lines l and m with the transversal t.
We have just shown that the alternate interior angles, $\angle XAB$ and $\angle ABY$, are equal.
According to the Converse of the Alternate Interior Angles Theorem, if two lines are cut by a transversal such that a pair of alternate interior angles is equal, then the two lines must be parallel.
Since $\angle XAB = \angle ABY$, we can conclude that the lines l and m are parallel.
l || m
Hence, proved.
Question 5. In Fig. 6.12, BA || ED and BC || EF. Show that ∠ABC = ∠DEF
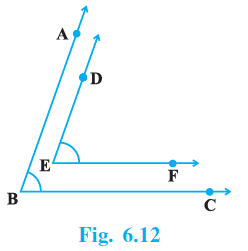
[Hint: Produce DE to intersect BC at P (say)].
Answer:
Given:
BA || ED
BC || EF
To Prove:
$\angle ABC = \angle DEF$
Construction Required:
Produce the line segment DE to intersect the line segment BC at a point P.
Proof:
According to our construction, the line DP is an extension of the line ED. Since we are given BA || ED, it follows that BA || DP.
Now, consider the parallel lines BA and DP, and let BC be the transversal line intersecting them.
The angles $\angle ABC$ and $\angle DPC$ are corresponding angles. When two parallel lines are cut by a transversal, the corresponding angles are equal.
$\angle ABC = \angle DPC$
[Corresponding Angles] ... (i)
Next, we are given that BC || EF. The line segment PC is a part of the line BC, so we can say PC || EF.
Consider the parallel lines PC and EF, and let DE (or DP) be the transversal line intersecting them.
The angles $\angle DPC$ and $\angle DEF$ are also corresponding angles.
$\angle DPC = \angle DEF$
[Corresponding Angles] ... (ii)
Now, by comparing equation (i) and equation (ii), we can see that both $\angle ABC$ and $\angle DEF$ are equal to the same angle, $\angle DPC$.
Therefore, we can conclude that:
$\angle ABC = \angle DEF$
[Things which are equal to the same thing are equal to one another]
Hence, proved.
Question 6. In Fig. 6.13, BA || ED and BC || EF. Show that ∠ ABC + ∠ DEF = 180°
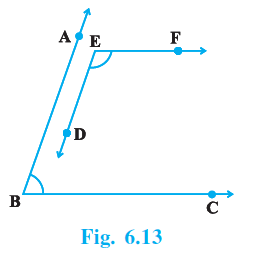
Answer:
Given:
In the given figure, we have:
BA || ED
BC || EF
To Prove:
$\angle ABC + \angle DEF = 180^\circ$
Construction Required:
Produce the ray EF backwards to intersect the ray BA at a point G.
Proof:
From our construction, the line GE is an extension of the line EF. Since we are given BC || EF, it follows that BC || GE.
Now, consider the parallel lines BC and GE, and let BA (or BG) be the transversal intersecting them.
The angles $\angle ABC$ and $\angle BGE$ are interior angles on the same side of the transversal (consecutive interior angles). The sum of consecutive interior angles is $180^\circ$.
$\angle ABC + \angle BGE = 180^\circ$
[Consecutive Interior Angles] ... (i)
Next, we are given that BA || ED. The line segment BG is part of the line BA, so we can say BG || ED.
Consider the parallel lines BG and ED, and let GE be the transversal intersecting them.
The angles $\angle BGE$ and $\angle DEF$ are corresponding angles. When two parallel lines are cut by a transversal, the corresponding angles are equal.
$\angle BGE = \angle DEF$
[Corresponding Angles] ... (ii)
Now, substitute the value of $\angle BGE$ from equation (ii) into equation (i):
$\angle ABC + \angle DEF = 180^\circ$
Hence, proved.
Question 7. In Fig. 6.14, DE || QR and AP and BP are bisectors of ∠ EAB and ∠ RBA,respectively. Find ∠APB.
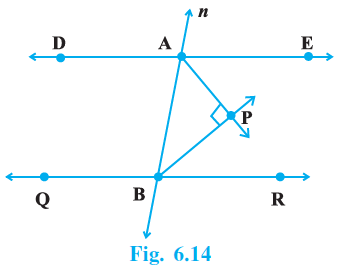
Answer:
Given:
DE || QR
AP is the bisector of $\angle EAB$.
BP is the bisector of $\angle RBA$.
To Find:
$\angle APB$
Solution:
Since DE || QR and AB is a transversal, the sum of consecutive interior angles is $180^\circ$.
$\angle EAB + \angle RBA = 180^\circ$
[Consecutive Interior Angles]
Since AP is the bisector of $\angle EAB$, we have:
$\angle PAB = \frac{1}{2}\angle EAB$
... (i)
Since BP is the bisector of $\angle RBA$, we have:
$\angle PBA = \frac{1}{2}\angle RBA$
... (ii)
In $\triangle APB$, the sum of interior angles is $180^\circ$.
$\angle APB + \angle PAB + \angle PBA = 180^\circ$
[Angle Sum Property of a Triangle]
Substitute the values from (i) and (ii) into the equation:
$\angle APB + \frac{1}{2}\angle EAB + \frac{1}{2}\angle RBA = 180^\circ$
$\angle APB + \frac{1}{2}(\angle EAB + \angle RBA) = 180^\circ$
From the property of consecutive interior angles, we know that $\angle EAB + \angle RBA = 180^\circ$. Substituting this value:
$\angle APB + \frac{1}{2}(180^\circ) = 180^\circ$
$\angle APB + 90^\circ = 180^\circ$
Solving for $\angle APB$:
$\angle APB = 180^\circ - 90^\circ$
$\angle APB = 90^\circ$
Therefore, $\angle APB = 90^\circ$.
Question 8. The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
Answer:
Given:
The angles of a triangle are in the ratio 2 : 3 : 4.
To Find:
The measure of each angle of the triangle.
Solution:
Let the angles of the triangle be $2x$, $3x$, and $4x$, where $x$ is a common multiple.
The sum of the angles in a triangle is $180^\circ$ (Angle Sum Property of a Triangle).
$2x + 3x + 4x = 180^\circ$
[Angle Sum Property]
Combine the terms on the left side:
$(2 + 3 + 4)x = 180^\circ$
$9x = 180^\circ$
Now, solve for $x$:
$x = \frac{180^\circ}{9}$
$x = 20^\circ$
Now, find the measure of each angle:
First angle $= 2x = 2(20^\circ) = 40^\circ$
Second angle $= 3x = 3(20^\circ) = 60^\circ$
Third angle $= 4x = 4(20^\circ) = 80^\circ$
To verify, check the sum of the angles: $40^\circ + 60^\circ + 80^\circ = 180^\circ$. The sum is correct.
The ratio of the angles is $40^\circ : 60^\circ : 80^\circ = 4 : 6 : 8 = 2 : 3 : 4$, which matches the given ratio.
The angles of the triangle are $40^\circ$, $60^\circ$, and $80^\circ$.
Question 9. A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠ BAL = ∠ ACB.
Answer:
Given:
A triangle ABC which is right-angled at A. This means $\angle BAC = 90^\circ$.
L is a point on the side BC such that AL is perpendicular to BC. This means $\angle ALC = 90^\circ$ and $\angle ALB = 90^\circ$.
To Prove:
$\angle BAL = \angle ACB$
Proof:
First, let's consider the large right-angled triangle, $\triangle ABC$.
By the angle sum property of a triangle, the sum of all interior angles is $180^\circ$.
$\angle BAC + \angle ABC + \angle ACB = 180^\circ$
We are given that $\angle BAC = 90^\circ$. Substituting this value:
$90^\circ + \angle ABC + \angle ACB = 180^\circ$
$\angle ABC + \angle ACB = 180^\circ - 90^\circ$
$\angle ABC + \angle ACB = 90^\circ$
... (i)
From this, we can write $\angle ACB$ as:
$\angle ACB = 90^\circ - \angle ABC$
... (ii)
Now, let's consider the smaller right-angled triangle, $\triangle ALB$.
We know that $\angle ALB = 90^\circ$ (since AL ⊥ BC).
Applying the angle sum property to $\triangle ALB$:
$\angle ALB + \angle ABL + \angle BAL = 180^\circ$
Note that $\angle ABL$ is the same angle as $\angle ABC$.
$90^\circ + \angle ABC + \angle BAL = 180^\circ$
$\angle ABC + \angle BAL = 180^\circ - 90^\circ$
$\angle ABC + \angle BAL = 90^\circ$
From this, we can write $\angle BAL$ as:
$\angle BAL = 90^\circ - \angle ABC$
... (iii)
By comparing equation (ii) and equation (iii), we can see that both $\angle ACB$ and $\angle BAL$ are equal to the same expression ($90^\circ - \angle ABC$).
Therefore, we can conclude:
$\angle BAL = \angle ACB$
Hence, proved.
Alternate Solution:
We are given that $\angle BAC = 90^\circ$. From the figure, we can see that $\angle BAC$ is composed of two adjacent angles, $\angle BAL$ and $\angle LAC$.
$\angle BAL + \angle LAC = \angle BAC$
$\angle BAL + \angle LAC = 90^\circ$
... (a)
Now, let's consider the right-angled triangle $\triangle ALC$.
We know that $\angle ALC = 90^\circ$. By the angle sum property of a triangle:
$\angle ALC + \angle LAC + \angle ACL = 180^\circ$
Note that $\angle ACL$ is the same angle as $\angle ACB$.
$90^\circ + \angle LAC + \angle ACB = 180^\circ$
$\angle LAC + \angle ACB = 180^\circ - 90^\circ$
$\angle LAC + \angle ACB = 90^\circ$
... (b)
From equation (a) and equation (b), both expressions are equal to $90^\circ$. So, we can equate them:
$\angle BAL + \angle LAC = \angle LAC + \angle ACB$
Subtracting the common angle $\angle LAC$ from both sides, we get:
$\angle BAL = \angle ACB$
Hence, proved.
Question 10. Two lines are respectively perpendicular to two parallel lines. Show that they are parallel to each other.
Answer:
Given:
There are four lines, let's call them l, m, p, and q.
l || m
(Line l is parallel to line m)
p ⊥ l
(Line p is perpendicular to line l)
q ⊥ m
(Line q is perpendicular to line m)
To Prove:
The lines p and q are parallel to each other.
p || q
Proof:
We are given that line l is parallel to line m, and line q is a transversal intersecting them.
l || m
[Given]
Let the angle formed by the intersection of line q and line m be $\angle 1$.
Since q ⊥ m, this angle is a right angle.
$\angle 1 = 90^\circ$
[Given]
Let the angle formed by the intersection of line q and line l be $\angle 2$.
Since l || m and q is the transversal, the consecutive interior angles ($\angle 1$ and $\angle 2$) are supplementary, meaning their sum is $180^\circ$.
$\angle 1 + \angle 2 = 180^\circ$
[Consecutive Interior Angles]
Substituting the value of $\angle 1$:
$90^\circ + \angle 2 = 180^\circ$
$\angle 2 = 180^\circ - 90^\circ$
$\angle 2 = 90^\circ$
This means that line q is also perpendicular to line l.
q ⊥ l
... (i)
We are also given that:
p ⊥ l
[Given] ... (ii)
From (i) and (ii), we can see that both lines p and q are perpendicular to the same line, l.
There is a theorem which states that two lines that are perpendicular to the same line are parallel to each other.
Therefore, based on this theorem, we can conclude that:
p || q
Hence, proved.
Sample Question 1 to 3 (Before Exercise 6.4)
Sample Question 1: In Fig. 6.15, m and n are two plane mirrors perpendicular to each other. Show that incident ray CA is parallel to reflected ray BD.

Answer:
Given:
Two plane mirrors, m and n, are placed perpendicular to each other.
An incident ray CA strikes mirror n at A, gets reflected as ray AB, which strikes mirror m at B, and finally gets reflected as ray BD.
m ⊥ n
To Prove:
The incident ray CA is parallel to the final reflected ray BD.
CA || BD
Proof:
Let AP be the normal to the mirror n at the point of incidence A, and let BP be the normal to the mirror m at the point of incidence B. A normal is a line perpendicular to the surface at that point.
AP ⊥ n
and
BP ⊥ m
According to the laws of reflection, the angle of incidence is equal to the angle of reflection.
For the reflection at point A on mirror n:
$\angle 1 = \angle 2$
[Angle of incidence = Angle of reflection] ... (i)
For the reflection at point B on mirror m:
$\angle 3 = \angle 4$
[Angle of incidence = Angle of reflection] ... (ii)
Since the mirror m is perpendicular to mirror n, the normals AP and BP drawn to them will also be perpendicular to each other. Let's prove this by considering the quadrilateral OAPB (where O is the point of intersection of the mirrors).
In quadrilateral OAPB:
$\angle AOB = 90^\circ$
[Given m ⊥ n]
$\angle OAP = 90^\circ$
[Since AP ⊥ n]
$\angle OBP = 90^\circ$
[Since BP ⊥ m]
The sum of the angles in a quadrilateral is $360^\circ$.
$\angle AOB + \angle OAP + \angle APB + \angle OBP = 360^\circ$
$90^\circ + 90^\circ + \angle APB + 90^\circ = 360^\circ$
$270^\circ + \angle APB = 360^\circ$
$\angle APB = 360^\circ - 270^\circ = 90^\circ$
Now, consider the triangle $\triangle APB$. The sum of its interior angles is $180^\circ$.
$\angle PAB + \angle PBA + \angle APB = 180^\circ$
From the figure, $\angle PAB = \angle 2$ and $\angle PBA = \angle 3$.
$\angle 2 + \angle 3 + 90^\circ = 180^\circ$
$\angle 2 + \angle 3 = 180^\circ - 90^\circ$
$\angle 2 + \angle 3 = 90^\circ$
... (iii)
To prove that CA || BD, we will consider AB as a transversal. We need to show that the sum of the consecutive interior angles, $\angle CAB$ and $\angle ABD$, is $180^\circ$.
From the figure, we have:
$\angle CAB = \angle 1 + \angle 2$
$\angle ABD = \angle 3 + \angle 4$
Sum of consecutive interior angles = $\angle CAB + \angle ABD = (\angle 1 + \angle 2) + (\angle 3 + \angle 4)$
Using equations (i) and (ii), we can substitute $\angle 1 = \angle 2$ and $\angle 3 = \angle 4$:
Sum = $(\angle 2 + \angle 2) + (\angle 3 + \angle 3)$
Sum = $2\angle 2 + 2\angle 3$
Sum = $2(\angle 2 + \angle 3)$
Now, using equation (iii), we substitute $\angle 2 + \angle 3 = 90^\circ$:
Sum = $2(90^\circ)$
Sum = $180^\circ$
So, we have shown that $\angle CAB + \angle ABD = 180^\circ$.
According to the Converse of the Consecutive Interior Angles Theorem, if two lines are intersected by a transversal such that the sum of the interior angles on the same side is $180^\circ$, then the lines are parallel.
Therefore, CA || BD.
Hence, proved.
Sample Question 2: Prove that the sum of the three angles of a triangle is 180°.
Answer:
This is a fundamental theorem in geometry known as the Angle Sum Property of a Triangle.
Given:
A triangle, let's call it $\triangle ABC$.
To Prove:
The sum of the interior angles of $\triangle ABC$ is $180^\circ$.
That is, $\angle BAC + \angle ABC + \angle BCA = 180^\circ$.
Construction Required:
Draw a line XY through the vertex A such that the line XY is parallel to the opposite side BC.
Proof:
Let's label the angles for clarity:
Let $\angle 1 = \angle BAC$
Let $\angle 2 = \angle ABC$
Let $\angle 3 = \angle BCA$
Let $\angle 4 = \angle XAB$
Let $\angle 5 = \angle YAC$
By our construction, XY is a straight line. The angles on a straight line at point A add up to $180^\circ$.
$\angle XAB + \angle BAC + \angle YAC = 180^\circ$
[Angles on a straight line]
Using our labels, this can be written as:
$\angle 4 + \angle 1 + \angle 5 = 180^\circ$
... (i)
Now, since we constructed XY to be parallel to BC (XY || BC), we can use the properties of parallel lines with transversals.
Consider AB as a transversal intersecting the parallel lines XY and BC.
The angles $\angle XAB$ and $\angle ABC$ form a pair of alternate interior angles. Therefore, they are equal.
$\angle XAB = \angle ABC$
[Alternate interior angles]
$\angle 4 = \angle 2$
... (ii)
Now, consider AC as a transversal intersecting the parallel lines XY and BC.
The angles $\angle YAC$ and $\angle BCA$ also form a pair of alternate interior angles. Therefore, they are equal.
$\angle YAC = \angle BCA$
[Alternate interior angles]
$\angle 5 = \angle 3$
... (iii)
Now, we substitute the results from (ii) and (iii) into equation (i).
In equation (i), we replace $\angle 4$ with $\angle 2$, and we replace $\angle 5$ with $\angle 3$.
$\angle 2 + \angle 1 + \angle 3 = 180^\circ$
Rearranging the terms, we get:
$\angle 1 + \angle 2 + \angle 3 = 180^\circ$
Substituting the original angle names back, we have:
$\angle BAC + \angle ABC + \angle BCA = 180^\circ$
Hence, it is proved that the sum of the three angles of a triangle is $180^\circ$.
Sample Question 3: Bisectors of angles B and C of a triangle ABC intersect each other at the point O. Prove that ∠BOC = 90° + $\frac{1}{2}$ ∠A
Answer:
Given:
A triangle ABC.
The bisector of $\angle B$ (ray BO) and the bisector of $\angle C$ (ray CO) intersect each other at point O.
To Prove:
$\angle BOC = 90^\circ + \frac{1}{2} \angle A$
Proof:
First, let's consider the main triangle, $\triangle ABC$.
According to the angle sum property of a triangle, the sum of all its interior angles is $180^\circ$.
$\angle A + \angle B + \angle C = 180^\circ$
[Angle Sum Property of a Triangle] ... (i)
Now, let's consider the smaller triangle, $\triangle BOC$.
Applying the angle sum property to $\triangle BOC$:
$\angle BOC + \angle OBC + \angle OCB = 180^\circ$
... (ii)
We are given that BO is the bisector of $\angle B$. This means it divides $\angle B$ into two equal angles.
$\angle OBC = \frac{1}{2} \angle B$
Similarly, we are given that CO is the bisector of $\angle C$.
$\angle OCB = \frac{1}{2} \angle C$
Now, substitute these expressions for $\angle OBC$ and $\angle OCB$ into equation (ii):
$\angle BOC + \frac{1}{2} \angle B + \frac{1}{2} \angle C = 180^\circ$
$\angle BOC + \frac{1}{2} (\angle B + \angle C) = 180^\circ$
Let's isolate $\angle BOC$:
$\angle BOC = 180^\circ - \frac{1}{2} (\angle B + \angle C)$
... (iii)
From our first equation (i), we can express $(\angle B + \angle C)$ in terms of $\angle A$:
$\angle B + \angle C = 180^\circ - \angle A$
Now, substitute this expression for $(\angle B + \angle C)$ into equation (iii):
$\angle BOC = 180^\circ - \frac{1}{2} (180^\circ - \angle A)$
Distribute the $\frac{1}{2}$ inside the parenthesis:
$\angle BOC = 180^\circ - (\frac{180^\circ}{2} - \frac{1}{2} \angle A)$
$\angle BOC = 180^\circ - (90^\circ - \frac{1}{2} \angle A)$
$\angle BOC = 180^\circ - 90^\circ + \frac{1}{2} \angle A$
Simplifying the expression gives us the desired result:
$\angle BOC = 90^\circ + \frac{1}{2} \angle A$
Hence, proved.
Exercise 6.4
Question 1. If two lines intersect, prove that the vertically opposite angles are equal.
Answer:
Given:
Two lines, let's call them AB and CD, intersect each other at a point O.
This intersection forms two pairs of vertically opposite angles: ($\angle AOC$, $\angle BOD$) and ($\angle AOD$, $\angle BOC$).
To Prove:
The vertically opposite angles are equal.
i.e., $\angle AOC = \angle BOD$ and $\angle AOD = \angle BOC$.
Proof:
First, let's consider the straight line AB. The ray OC stands on this line.
The angles $\angle AOC$ and $\angle BOC$ form a linear pair. By the Linear Pair Axiom, their sum is $180^\circ$.
$\angle AOC + \angle BOC = 180^\circ$
[Linear Pair Axiom] ... (i)
Now, let's consider the straight line CD. The ray OB stands on this line.
The angles $\angle BOC$ and $\angle BOD$ also form a linear pair. Therefore, their sum is $180^\circ$.
$\angle BOC + \angle BOD = 180^\circ$
[Linear Pair Axiom] ... (ii)
From equation (i) and equation (ii), we can see that both expressions are equal to $180^\circ$. Therefore, we can equate them:
$\angle AOC + \angle BOC = \angle BOC + \angle BOD$
Subtracting the common angle $\angle BOC$ from both sides of the equation, we get:
$\angle AOC = \angle BOD$
This proves that one pair of vertically opposite angles is equal.
Similarly, we can prove that the other pair is equal.
Consider the straight line AB again. The ray OD stands on it.
$\angle AOD + \angle BOD = 180^\circ$
[Linear Pair Axiom] ... (iii)
From equation (ii) and (iii), we can equate the expressions:
$\angle BOC + \angle BOD = \angle AOD + \angle BOD$
Subtracting the common angle $\angle BOD$ from both sides, we get:
$\angle BOC = \angle AOD$
This proves that the second pair of vertically opposite angles is also equal.
Hence, it is proved that when two lines intersect, the vertically opposite angles are equal.
Question 2. Bisectors of interior ∠B and exterior ∠ACD of a ∆ ABC intersect at the point T. Prove that ∠ BTC = $\frac{1}{2}$ ∠ BAC.
Answer:
Given:
In a triangle $\triangle ABC$, the side BC is extended to a point D.
BT is the bisector of the interior angle $\angle ABC$.
CT is the bisector of the exterior angle $\angle ACD$.
The bisectors BT and CT intersect at the point T.
To Prove:
$\angle BTC = \frac{1}{2} \angle BAC$.
Proof:
Let's consider the triangle $\triangle BTC$. The angle $\angle TCD$ is an exterior angle to this triangle.
By the Exterior Angle Theorem, an exterior angle of a triangle is equal to the sum of its two interior opposite angles.
$\angle TCD = \angle BTC + \angle TBC$
[Exterior Angle Theorem on $\triangle BTC$] ... (i)
We are given that BT is the bisector of $\angle ABC$. Therefore:
$\angle TBC = \frac{1}{2} \angle ABC$
Substituting this into equation (i):
$\angle TCD = \angle BTC + \frac{1}{2} \angle ABC$
... (ii)
Now, let's consider the main triangle, $\triangle ABC$. The angle $\angle ACD$ is an exterior angle.
Applying the Exterior Angle Theorem to $\triangle ABC$:
$\angle ACD = \angle BAC + \angle ABC$
[Exterior Angle Theorem on $\triangle ABC$]
We are given that CT is the bisector of $\angle ACD$. Therefore:
$\angle TCD = \frac{1}{2} \angle ACD$
Substituting the expression for $\angle ACD$ into this equation:
$\angle TCD = \frac{1}{2} (\angle BAC + \angle ABC)$
$\angle TCD = \frac{1}{2} \angle BAC + \frac{1}{2} \angle ABC$
... (iii)
Now we have two expressions for $\angle TCD$ from equations (ii) and (iii). We can equate them:
$\angle BTC + \frac{1}{2} \angle ABC = \frac{1}{2} \angle BAC + \frac{1}{2} \angle ABC$
Subtracting the common term $\frac{1}{2} \angle ABC$ from both sides of the equation:
$\angle BTC = \frac{1}{2} \angle BAC$
Hence, proved.
Question 3. A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
Answer:
Given:
Two parallel lines, AB and CD, are intersected by a transversal line, XY.
The transversal XY intersects the line AB at point P and the line CD at point Q.
Let PR be the bisector of a corresponding angle, $\angle XPB$.
Let QS be the bisector of the other corresponding angle, $\angle PQD$.
AB || CD
To Prove:
The bisectors PR and QS are parallel to each other.
PR || QS
Proof:
Since the line AB is parallel to the line CD and they are intersected by the transversal XY, the corresponding angles formed are equal.
$\angle XPB = \angle PQD$
[Corresponding Angles] ... (i)
We are given that the ray PR is the bisector of $\angle XPB$. This means PR divides the angle into two equal halves.
$\angle XPR = \frac{1}{2} \angle XPB$
... (ii)
Similarly, we are given that the ray QS is the bisector of $\angle PQD$. This means QS divides the angle into two equal halves.
$\angle PQS = \frac{1}{2} \angle PQD$
... (iii)
From equation (i), we know that the full corresponding angles are equal. Therefore, their halves must also be equal.
$\frac{1}{2} \angle XPB = \frac{1}{2} \angle PQD$
Now, by substituting the expressions from equations (ii) and (iii) into the above equality, we get:
$\angle XPR = \angle PQS$
Let's consider the lines PR and QS, with the line XY as the transversal.
We have just proved that the angles $\angle XPR$ and $\angle PQS$ are equal. These two angles are corresponding angles with respect to the lines PR and QS and the transversal XY.
According to the Converse of the Corresponding Angles Postulate, if two lines are cut by a transversal such that a pair of corresponding angles is equal, then the two lines are parallel.
Since $\angle XPR = \angle PQS$, we can conclude that the lines PR and QS are parallel.
PR || QS
Hence, it is proved that the bisectors of any pair of corresponding angles are parallel.
Question 4. Prove that through a given point, we can draw only one perpendicular to a given line.
[Hint: Use proof by contradiction].
Answer:
Given:
A line, let's call it l, and a point P not on the line l.
To Prove:
There is one and only one line that passes through point P and is perpendicular to line l.
Proof (by contradiction):
We will start by assuming the opposite of what we want to prove. Let's assume that it is possible to draw two distinct perpendicular lines from the point P to the line l.
Let these two lines be PM and PN, where M and N are two distinct points on the line l.
Since PM is perpendicular to line l, the angle formed at M is a right angle.
$\angle PMN = 90^\circ$
[By assumption, PM ⊥ l]
Similarly, since PN is perpendicular to line l, the angle formed at N is also a right angle.
$\angle PNM = 90^\circ$
[By assumption, PN ⊥ l]
Now, consider the triangle formed by the points P, M, and N, which is $\triangle PMN$.
According to the Angle Sum Property of a Triangle, the sum of the interior angles of any triangle is $180^\circ$.
$\angle MPN + \angle PMN + \angle PNM = 180^\circ$
Substitute the values of the angles at M and N into this equation:
$\angle MPN + 90^\circ + 90^\circ = 180^\circ$
$\angle MPN + 180^\circ = 180^\circ$
Solving for $\angle MPN$, we get:
$\angle MPN = 180^\circ - 180^\circ$
$\angle MPN = 0^\circ$
An angle of $0^\circ$ means that the rays PM and PN coincide, which implies that the lines PM and PN are the same line. This also means that the points P, M, and N are collinear (lie on the same straight line).
This result contradicts our initial assumption that PM and PN are two distinct perpendicular lines.
Since our assumption leads to a contradiction, the assumption must be false.
Therefore, it is not possible to draw two distinct perpendiculars from a given point to a given line.
Hence, through a given point, we can draw only one perpendicular to a given line.
Question 5. Prove that two lines that are respectively perpendicular to two intersecting lines intersect each other.
[Hint: Use proof by contradiction].
Answer:
Given:
Let there be two lines, $l_1$ and $l_2$, that intersect each other.
Let there be two other lines, $m_1$ and $m_2$.
Line $m_1$ is perpendicular to line $l_1$ ($m_1 \perp l_1$).
Line $m_2$ is perpendicular to line $l_2$ ($m_2 \perp l_2$).
To Prove:
The lines $m_1$ and $m_2$ intersect each other.
Proof (by contradiction):
We will start by assuming the opposite of what we need to prove. Let us assume that the lines $m_1$ and $m_2$ do not intersect.
In a two-dimensional plane, if two distinct lines do not intersect, they must be parallel.
So, our assumption is that $m_1$ is parallel to $m_2$.
$m_1 \parallel m_2$
[Our Assumption]
Now, we use the given information. We are given that line $m_1$ is perpendicular to line $l_1$.
$m_1 \perp l_1$
[Given]
We have a theorem: "If a line is perpendicular to one of two parallel lines, then it is also perpendicular to the other."
Here, $l_1$ is perpendicular to $m_1$, and we have assumed $m_1 \parallel m_2$. Therefore, $l_1$ must also be perpendicular to $m_2$.
$l_1 \perp m_2$
... (i)
We are also given that line $m_2$ is perpendicular to line $l_2$.
$m_2 \perp l_2$
[Given]
This is the same as saying:
$l_2 \perp m_2$
... (ii)
From results (i) and (ii), we see that both lines $l_1$ and $l_2$ are perpendicular to the same line, $m_2$.
We know the theorem: "Two lines that are perpendicular to the same line are parallel to each other."
Since both $l_1$ and $l_2$ are perpendicular to $m_2$, it must be true that $l_1$ is parallel to $l_2$.
$l_1 \parallel l_2$
This conclusion, that $l_1$ is parallel to $l_2$, directly contradicts the given information that lines $l_1$ and $l_2$ intersect each other.
This contradiction arose because our initial assumption was incorrect.
Therefore, the assumption that "$m_1$ and $m_2$ do not intersect" must be false.
The only other possibility is that the lines $m_1$ and $m_2$ do intersect.
Hence, it is proved that two lines that are respectively perpendicular to two intersecting lines must intersect each other.
Question 6. Prove that a triangle must have atleast two acute angles.
Answer:
To Prove:
A triangle must have at least two acute angles.
(An acute angle is an angle with a measure less than $90^\circ$).
Proof (by contradiction):
Let us assume the contrary. We will assume that a triangle can have at most one acute angle. This assumption leads to two possible cases:
Case 1: The triangle has zero acute angles.
Case 2: The triangle has exactly one acute angle.
We will show that both cases lead to a contradiction with the fundamental Angle Sum Property of a Triangle, which states that the sum of the interior angles of any triangle is exactly $180^\circ$.
Case 1: The triangle has zero acute angles.
If a triangle has no acute angles, it means all three of its angles are either right ($90^\circ$) or obtuse (greater than $90^\circ$).
Let the angles of the triangle be $\angle A$, $\angle B$, and $\angle C$.
Then, we must have:
$\angle A \ge 90^\circ$
$\angle B \ge 90^\circ$
$\angle C \ge 90^\circ$
Let's find the sum of these three angles:
$\angle A + \angle B + \angle C \ge 90^\circ + 90^\circ + 90^\circ$
$\angle A + \angle B + \angle C \ge 270^\circ$
This result contradicts the Angle Sum Property, which states that the sum must be exactly $180^\circ$. Therefore, a triangle cannot have zero acute angles.
Case 2: The triangle has exactly one acute angle.
If a triangle has exactly one acute angle, then the other two angles must be either right or obtuse.
Let's say $\angle A$ is acute, so $\angle A < 90^\circ$. The other two angles, $\angle B$ and $\angle C$, must satisfy:
$\angle B \ge 90^\circ$
$\angle C \ge 90^\circ$
Let's find the sum of just these two angles:
$\angle B + \angle C \ge 90^\circ + 90^\circ$
$\angle B + \angle C \ge 180^\circ$
Now, let's find the sum of all three angles. Since $\angle A$ is an angle of a triangle, it must have a positive measure, so $\angle A > 0^\circ$.
$\angle A + \angle B + \angle C > 0^\circ + 180^\circ$
$\angle A + \angle B + \angle C > 180^\circ$
This result also contradicts the Angle Sum Property, which states that the sum must be exactly $180^\circ$. Therefore, a triangle cannot have exactly one acute angle.
Conclusion:
Both possible cases under our initial assumption lead to a contradiction. Therefore, our assumption that a triangle can have at most one acute angle is false.
The logical opposite of "at most one acute angle" is "at least two acute angles".
Hence, it is proved that a triangle must have at least two acute angles.
Question 7. In Fig. 6.17, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = $\frac{1}{2}$ ( ∠Q – ∠R).

Answer:
Given:
In $\triangle PQR$ shown in Fig. 6.17, we are given:
$\angle Q > \angle R$
PA is the bisector of $\angle QPR$
PM $\perp$ QR
To Prove:
$\angle APM = \frac{1}{2} (\angle Q – \angle R)$
Proof:
First, let's consider the right-angled triangle $\triangle PMQ$.
Since PM $\perp$ QR, we have $\angle PMQ = 90^\circ$.
By the angle sum property of a triangle, the sum of angles in $\triangle PMQ$ is $180^\circ$.
$\angle PMQ + \angle MQP + \angle QPM = 180^\circ$
Substituting the known values ($\angle MQP$ is the same as $\angle Q$):
$90^\circ + \angle Q + \angle QPM = 180^\circ$
$\angle QPM = 180^\circ - 90^\circ - \angle Q$
$\angle QPM = 90^\circ - \angle Q$
... (i)
Now, let's consider the main triangle, $\triangle PQR$.
By the angle sum property, we have:
$\angle QPR + \angle Q + \angle R = 180^\circ$
Solving for $\angle QPR$:
$\angle QPR = 180^\circ - (\angle Q + \angle R)$
We are given that PA is the bisector of $\angle QPR$. This means it divides the angle into two equal parts.
$\angle QPA = \frac{1}{2} \angle QPR$
Substituting the expression for $\angle QPR$:
$\angle QPA = \frac{1}{2} (180^\circ - (\angle Q + \angle R))$
$\angle QPA = 90^\circ - \frac{1}{2} (\angle Q + \angle R)$
... (ii)
From the figure, it is clear that the angle $\angle QPA$ is composed of two adjacent angles, $\angle QPM$ and $\angle APM$.
$\angle QPA = \angle QPM + \angle APM$
Rearranging to find $\angle APM$:
$\angle APM = \angle QPA - \angle QPM$
Now, substitute the expressions from equation (i) and equation (ii) into this relationship:
$\angle APM = \left(90^\circ - \frac{1}{2} (\angle Q + \angle R)\right) - (90^\circ - \angle Q)$
Distributing the terms:
$\angle APM = 90^\circ - \frac{1}{2}\angle Q - \frac{1}{2}\angle R - 90^\circ + \angle Q$
The $90^\circ$ terms cancel out. Combine the terms with $\angle Q$ and $\angle R$:
$\angle APM = \left(\angle Q - \frac{1}{2}\angle Q\right) - \frac{1}{2}\angle R$
$\angle APM = \frac{1}{2}\angle Q - \frac{1}{2}\angle R$
Factoring out $\frac{1}{2}$ gives the desired result:
$\angle APM = \frac{1}{2} (\angle Q - \angle R)$
Hence, proved.

